Highlights
Optimal Regularizers for a Data Source
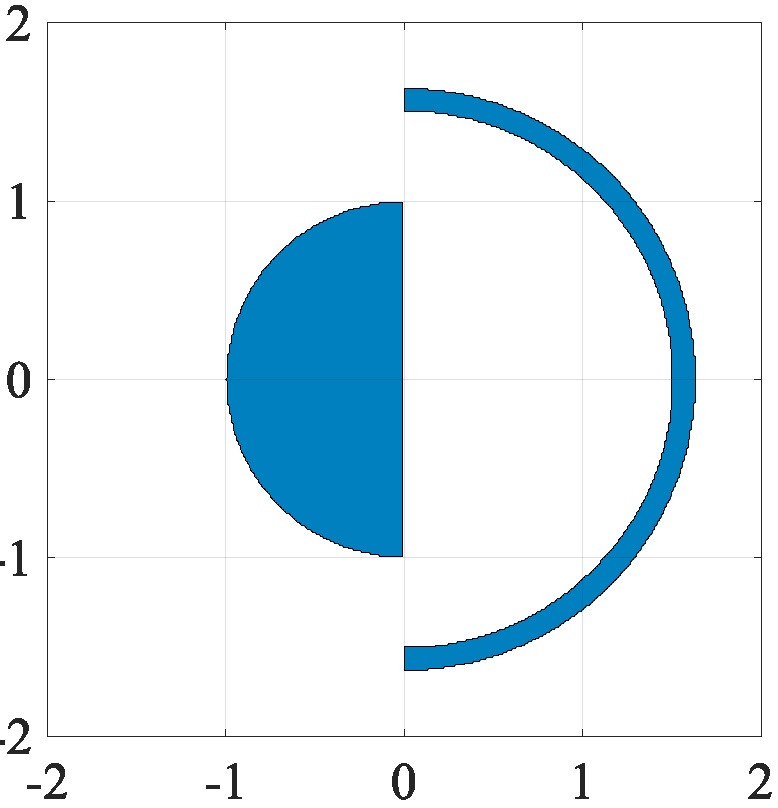
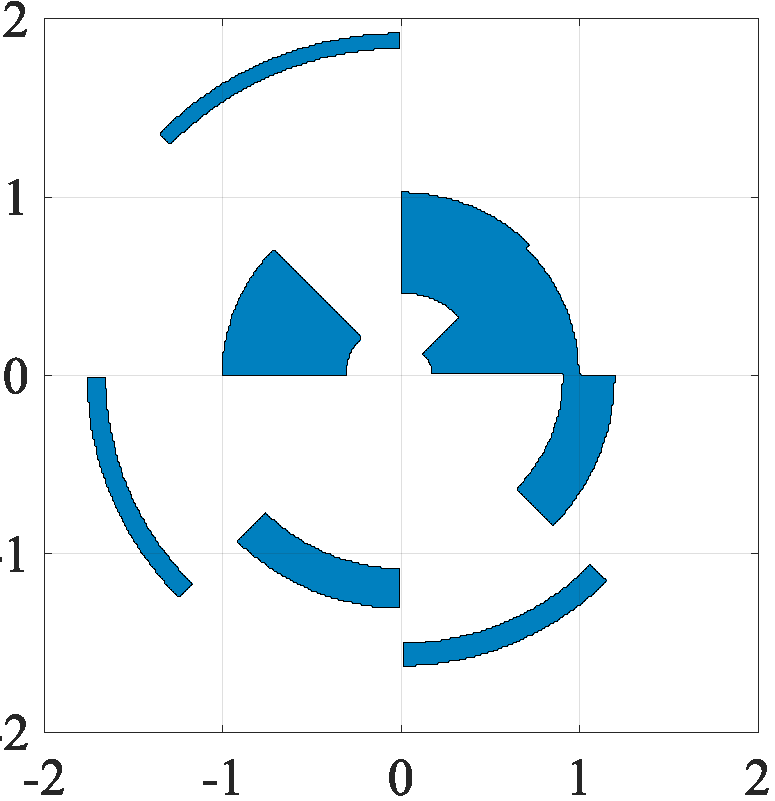
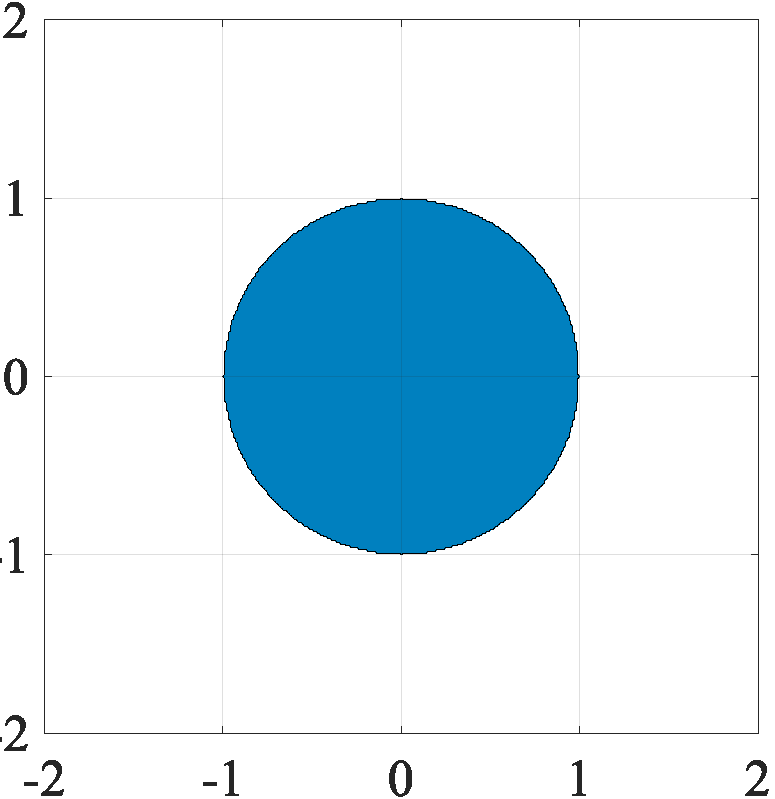
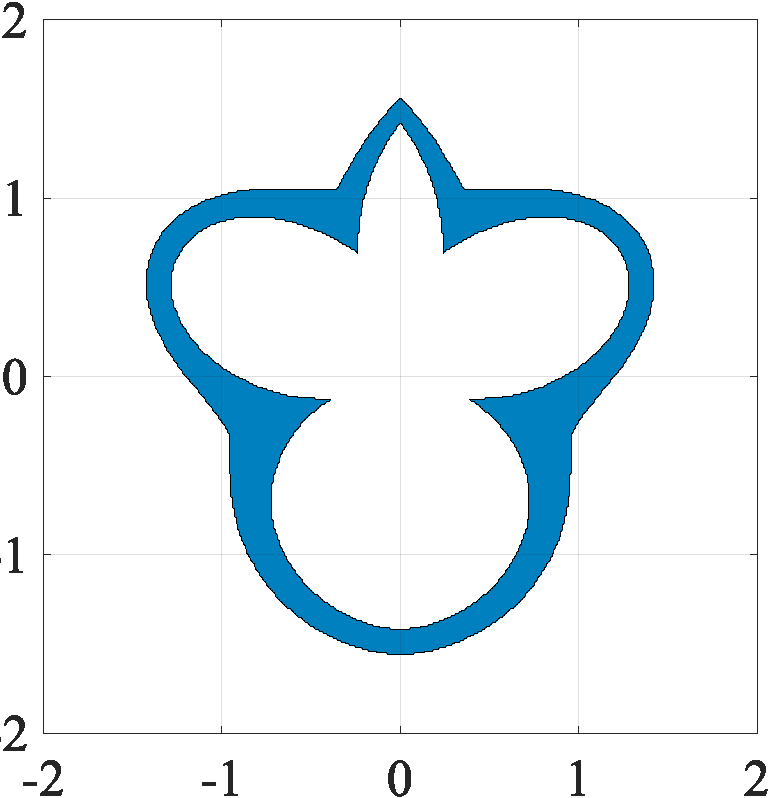
Regularizers are penalty functions that are frequently deployed in the context of solving inverse problems. These play an important role of addressing ill-posedness that might arise because of a lack of data, for instance. To give an illustration, if we believe that our data is well approximated as a sparse vector, then a reasonable choice of regularizer to apply is the L1-norm.
Regularization techniques are extremely powerful in practice – the difficulty of deploying such techniques is that we frequently do not know the appropriate choice of regularizer. In this line of work, we ask
Given a data source, can we identify the optimal choice of a regularization function for use, say, on a downstream task? How do we formulate such a conceptual problem into a mathematical question that is meaningful to us? How do computational considerations affect our preference for certain families of regularizers over others?
-
Optimal Convex and Nonconvex Regularizers for a Data Source, O. Leong, E. O’Reilly, Y. S. Soh, and V. Chandrasekaran, Foundations of Computational Mathematics (accepted), Dec ‘22, [arXiv]
-
The Star Geometry of Critic-Based Regularizer Learning, O. Leong, E. O’Reilly, Y. S. Soh, NeurIPS, Sep ‘24, [arXiv]
Graph Matching, Gromov-Wasserstein
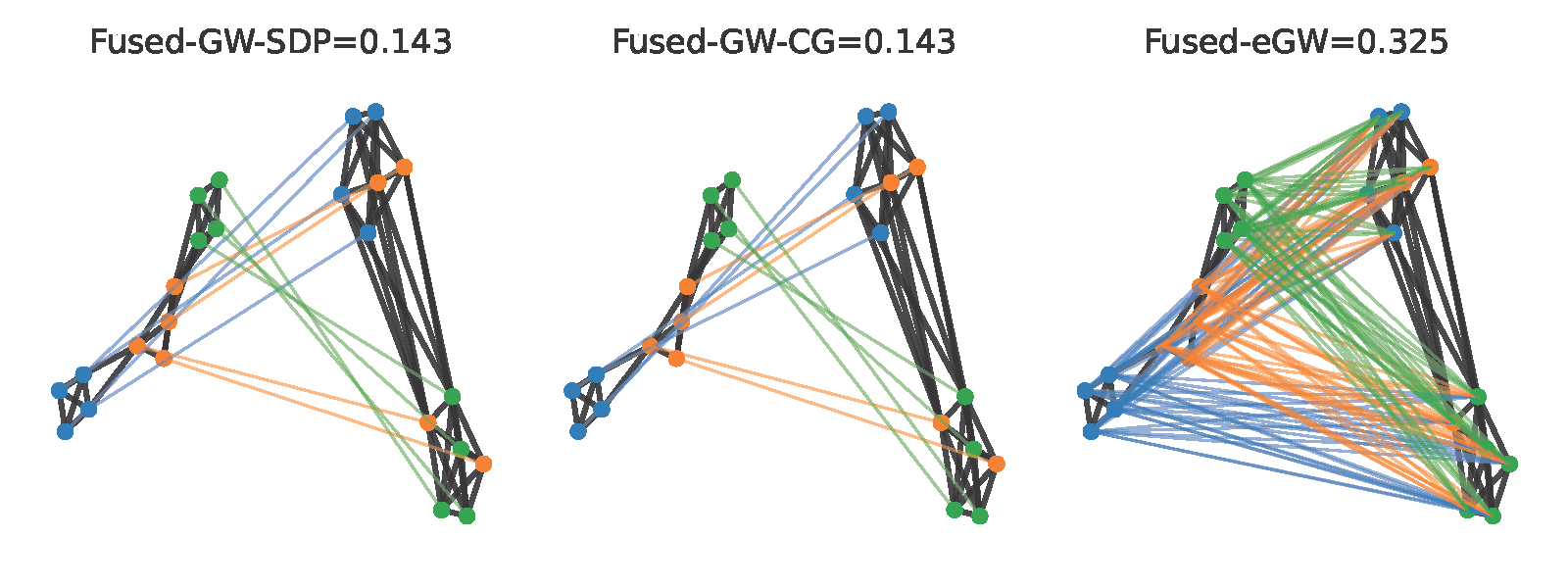
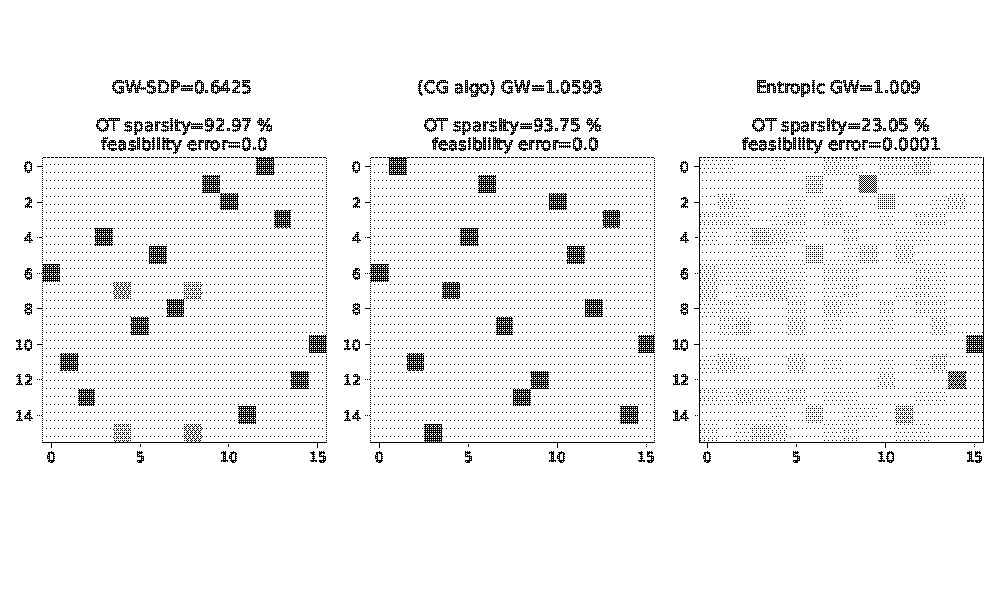

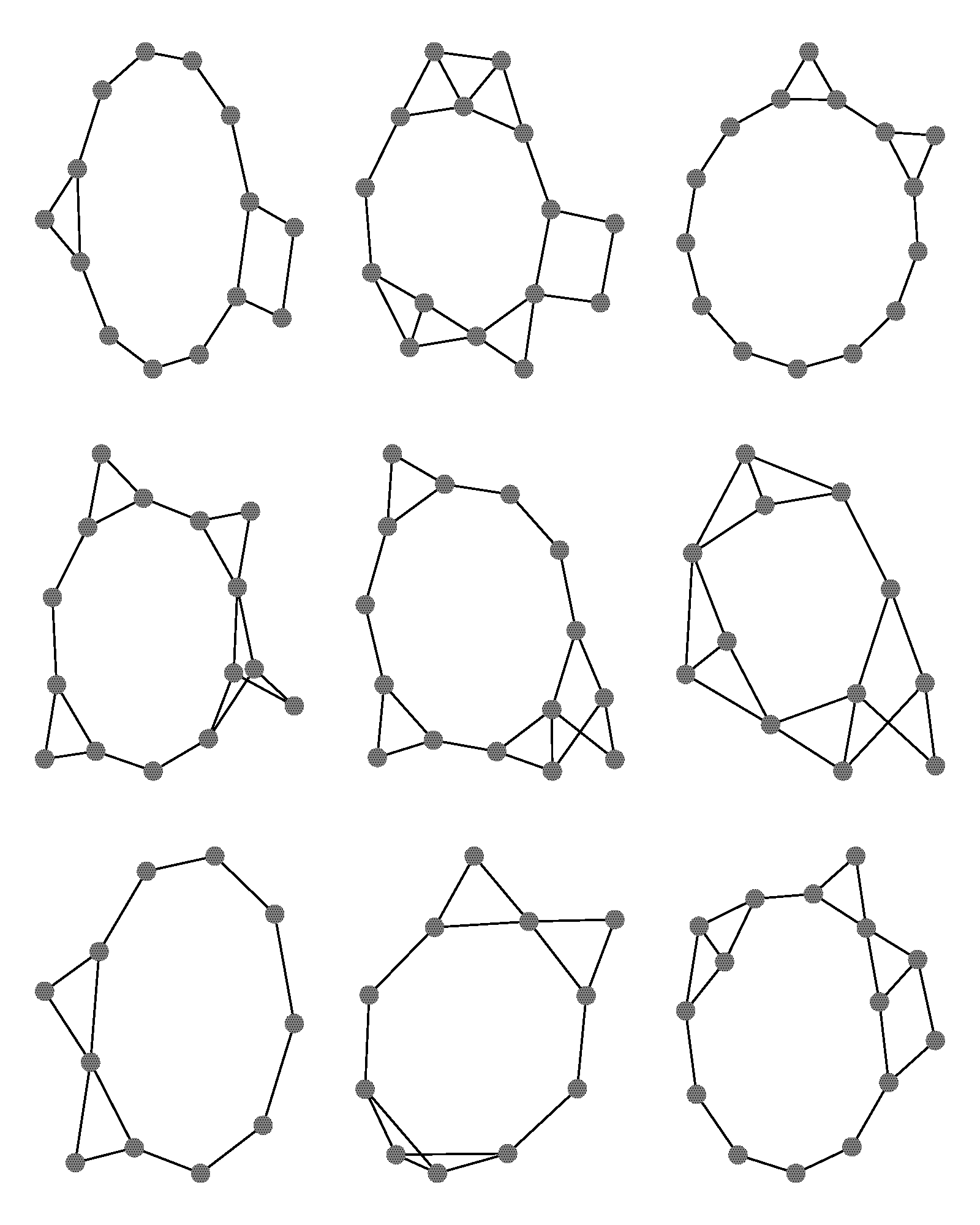
-
Sum-of-Squares Hierarchy for the Gromov-Wasserstein Problem, HA Tran, BT Nguyen, YS Soh, pre-print, Feb ‘25 [arXiv]
-
Exactness Conditions for Semidefinite Relaxations of the Quadratic Assignment Problem, J. Chen, Y. S. Soh, pre-print, Sep ‘24 [arXiv]
-
Semidefinite Relaxations of the Gromov-Wasserstein Distance, J. Chen, B. T. Nguyen, Y. S. Soh, NeurIPS ‘24, Dec ‘23, [arXiv]
-
The Lovasz Theta Function for Recovering Planted Clique Covers and Graph Colorings, J. Hou, Y. S. Soh, A. Varvitsiotis, pre-print, Oct ‘23, [arXiv]
Learning Data Representations with Symmetries
Suppose we want to learn a data representation for an image processing task. Ideally, the representation should be invariant to translations and rotations – after all, natural images still look like images after rotations! The basic question this line of work investigates is:
How do we learn data representations that incorporate these invariances in a principled manner?
Given a generic group, can I provide a general recipe that allows me to learn a data representation that respect these invariances automatically?
-
Dictionary Learning under Symmetries via Group Representations, S. Ghosh, A. Y. R. Low, Y. S. Soh, Z. Feng, B. K. Y. Tan, pre-print, Jun ‘23, [arXiv]
-
Group Invariant Dictionary Learning, Y. S. Soh, Transactions on Signal Processing, Jun ‘21, [Article] [arXiv] [Code] (maintained by Brendan KY Tan)
Fitting Convex Sets to Data


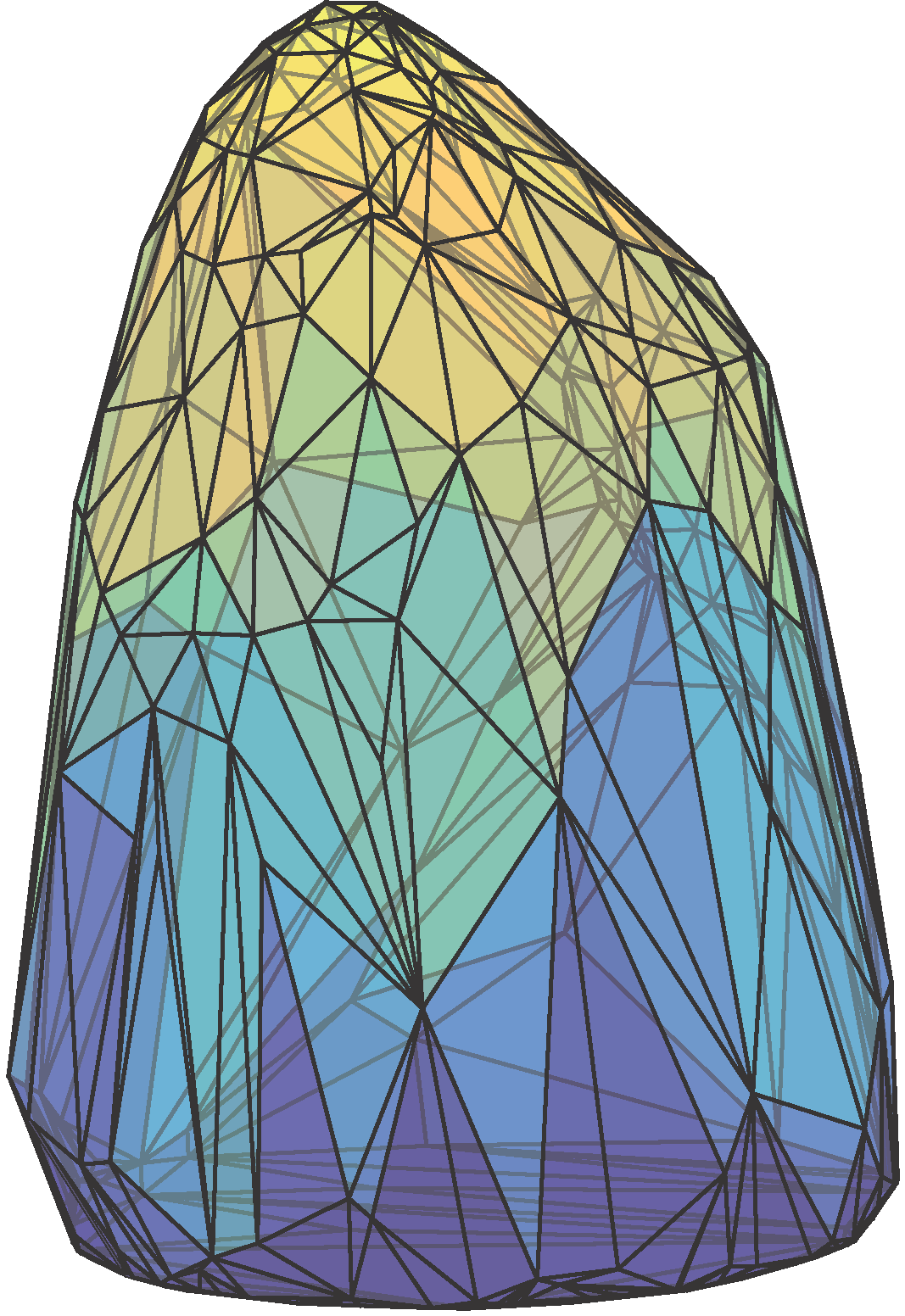

Given a collection of data-points in space, how do we fit a convex set or model to these points?
Firstly, why should we care? It turns out that a number of data processing problems can actually be viewed as the geometric task of fitting a convex set to data! Consider, for instance, the task of learning a regularizer for data-processing. For concreteness, we restrict to regularizers that are expressible via Linear Programming. It turns out that this process is known as dictionary learning or sparse coding in the literature.
Some of the key questions we ask:
What computational or data processing task can be viewed via a geometric lens as one of fitting a convex set to data?
How should we parameterize the convex set?
As it turns out, if we restrict to convex sets that are expressible via Linear Programs, we recover a number of existing methods (dictionary learning, sparse coding, non-negative matrix factorization, max-affine regression).
What happens if we consider fitting with convex sets that are expressible via semidefinite programming?
-
Fitting Tractable Convex Sets to Support Function Evaluations, Y. S. Soh and V. Chandrasekaran, Discrete and Computational Geometry, Jan ‘21, [Article] [arXiv] [Code]
-
Learning Semidefinite Regularizers, Y. S. Soh and V. Chandrasekaran, Foundations of Computational Mathematics, Mar ‘18, [Article] [arXiv] [Code]
-
Fitting Convex Sets to Data: Algorithms and Applications, Aug ‘18, PDF
Matrix Factorizations with Infinite Atoms
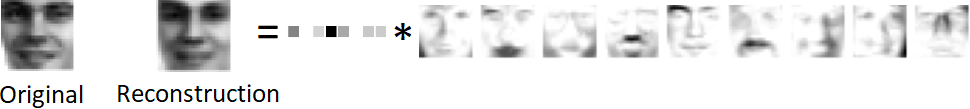
Given a data matrix Y, the matrix factorization task seeks a factorization of the form Y = A X, where A and X satisfies certain structural properties depending on the context. In the simplest example, we impose that A and X have small inner dimension, with no further restriction – this is simply the Singular Value Decomposition (SVD). If for instance, if one is interested in representing the data vectors in Y via a sparse basis, then one would impose (the columns of) X be sparse – this is known as dictionary learning or sparse coding. If instead one wishes to explain the data via non-negative components, then one seeks a non-negative matrix factorization.
One thing in common among these classical methods is that we compute a data matrix with finitely many atoms. However, there are settings in which this modelling assumption is inadequate – perhaps, depending on the data, it is beneficial to instead learn dictionaries that contain infinitely many atoms. The central question in these works are:
How do we learn matrix factorizations with infinitely many atoms? What does it mean to have dictionaries that have infinitely many atoms?
When is it beneficial to model data using infinitely large dictionaries?
-
Multiplicative Updates for Symmetric-cone Factorizations, Y. S. Soh and A. Varvitsiotis, Mathematical Programming Series A, [Article] [arXiv]
-
A Non-commutative Extension of Lee-Seung’s Algorithm for Positive Semidefinite Factorizations, Y. S. Soh and A. Varvitsiotis, NeurIPS, 2021 [arXiv] [Code]
-
Learning Semidefinite Regularizers, Y. S. Soh and V. Chandrasekaran, Foundations of Computational Mathematics, Mar ‘18, [Article] [arXiv] [Code]
-
Dictionary Learning under Symmetries via Group Representations, S. Ghosh, A. Y. R. Low, Y. S. Soh, Z. Feng, B. K. Y. Tan, pre-print, Jun ‘23, [arXiv]
-
Group Invariant Dictionary Learning, Y. S. Soh, Transactions on Signal Processing, Jun ‘21, [Article] [arXiv] [Code] (maintained by Brendan KY Tan)